There’s a way to spend less time managing your pay-per-click (PPC) ad campaigns while still getting a high return on your investment.
It’s called PPC automation. And it can save you time and improve your results.
In this article, you’ll learn how PPC ad automation works, how to create automated PPC campaigns, and which PPC automation tools to use.
Let’s start with the basics.
What Is PPC Automation?
PPC automation involves using specialized software to manage and optimize your pay-per-click ads automatically.
The tools adjust settings like ad spend, keyword selection, and ad placement (where your ads are displayed) based on real-time data and predictive analytics. Often with just minutes of your time.
This allows for more precise ad placement and timing. Which means you reach potential customers more efficiently and likely with lower PPC costs.
Benefits of PPC Automation
PPC ad automation can help you achieve your campaign goals faster and more cost-effectively. Here are some of its benefits:
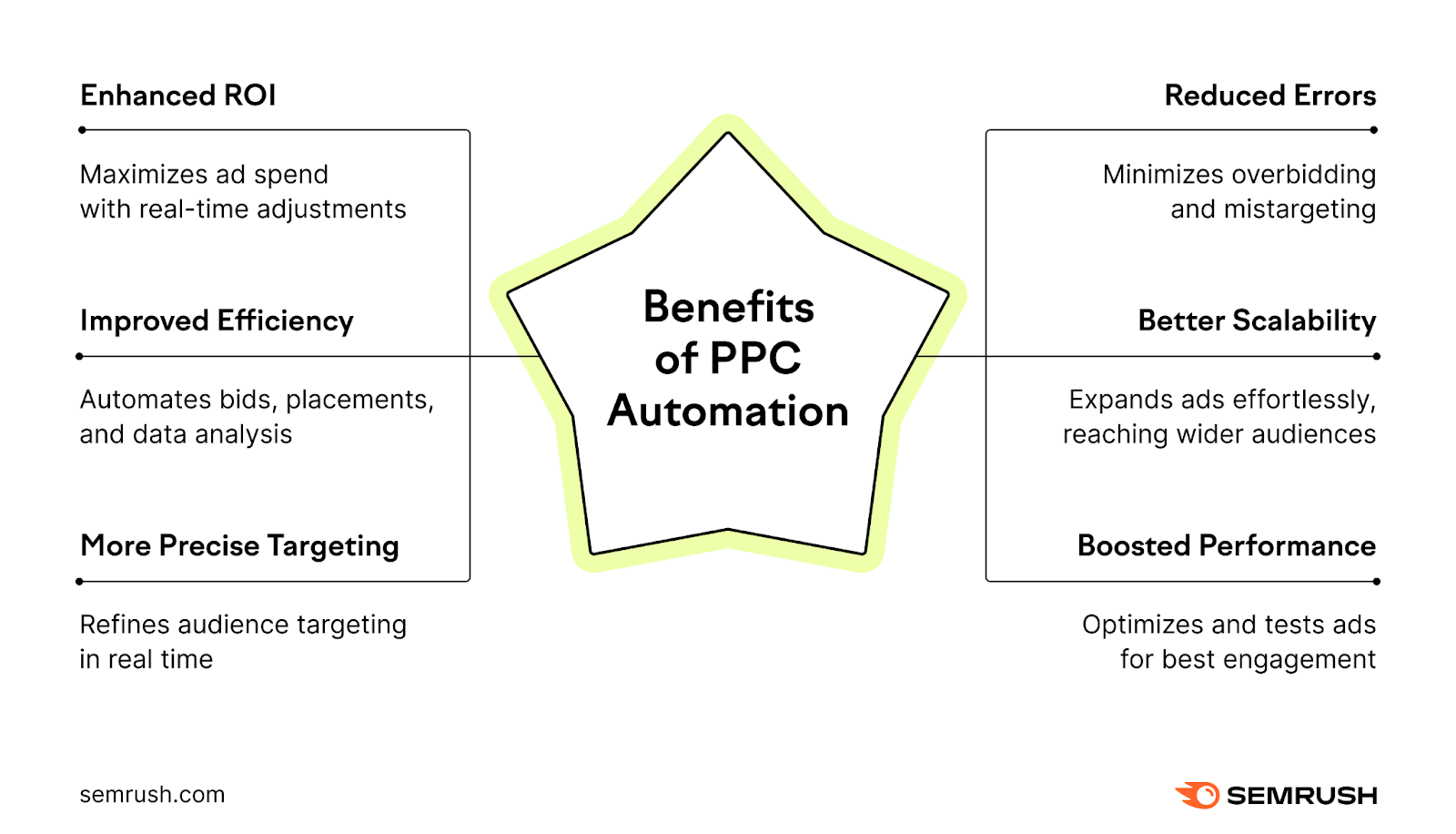
Enhanced ROI
Automation tools continuously monitor your ad performance, adjusting bids (the amount you’re willing to pay for a click) and placements in real time.
They ensure maximum visibility and engagement by directing your budget toward the best-performing ads.
The result? A higher return on investment (ROI) for every advertising dollar you spend.
Improved Efficiency
Instead of manually setting bids, selecting placements, or sifting through data, automation handles this for you.
It can evaluate keyword performance, tweak ad schedules (when your ads are shown), and pause ads that aren’t performing well.
Your campaigns remain optimized and you save time.
More Precise Targeting
Automation leverages data to fine-tune your audience targeting in real time. So you don’t have to go through the trouble of manually refining targeting criteria every hour or day based on recent ad performance.
It can analyze patterns like user behavior and search habits to ensure your ads are displayed to those most likely to take action.
Reduced Errors
Automation streamlines tasks like bid adjustments and ad placements. This minimizes human errors.
Whether it’s mitigating the risk of overbidding (paying too much) or mistargeting, automation can keep your campaigns on an error-free path.
Better Scalability
As you introduce more products or venture into new markets, the complexity of managing ads increases.
Automation tools can more effectively handle expansion.
They can help you manage more ads and reach broader audiences without adding stress. Ensuring your advertising efforts remain effective.
Now that you know the advantages of PPC automation, let’s talk about how you can automate PPC campaigns.
PPC Campaign Elements You Can Automate
Running a PPC campaign is a process with multiple components. From research to budget management to reporting.
Let’s take an example of Google Ads. Here are five important components you can automate:
Bidding
Manually managing bids is time-consuming. It also leaves room for inconsistencies and oversights.
Consider the challenge of manually tracking hundreds of keywords across a variety of search ad campaigns—each with unique performance metrics and competition. The task would be enormous.
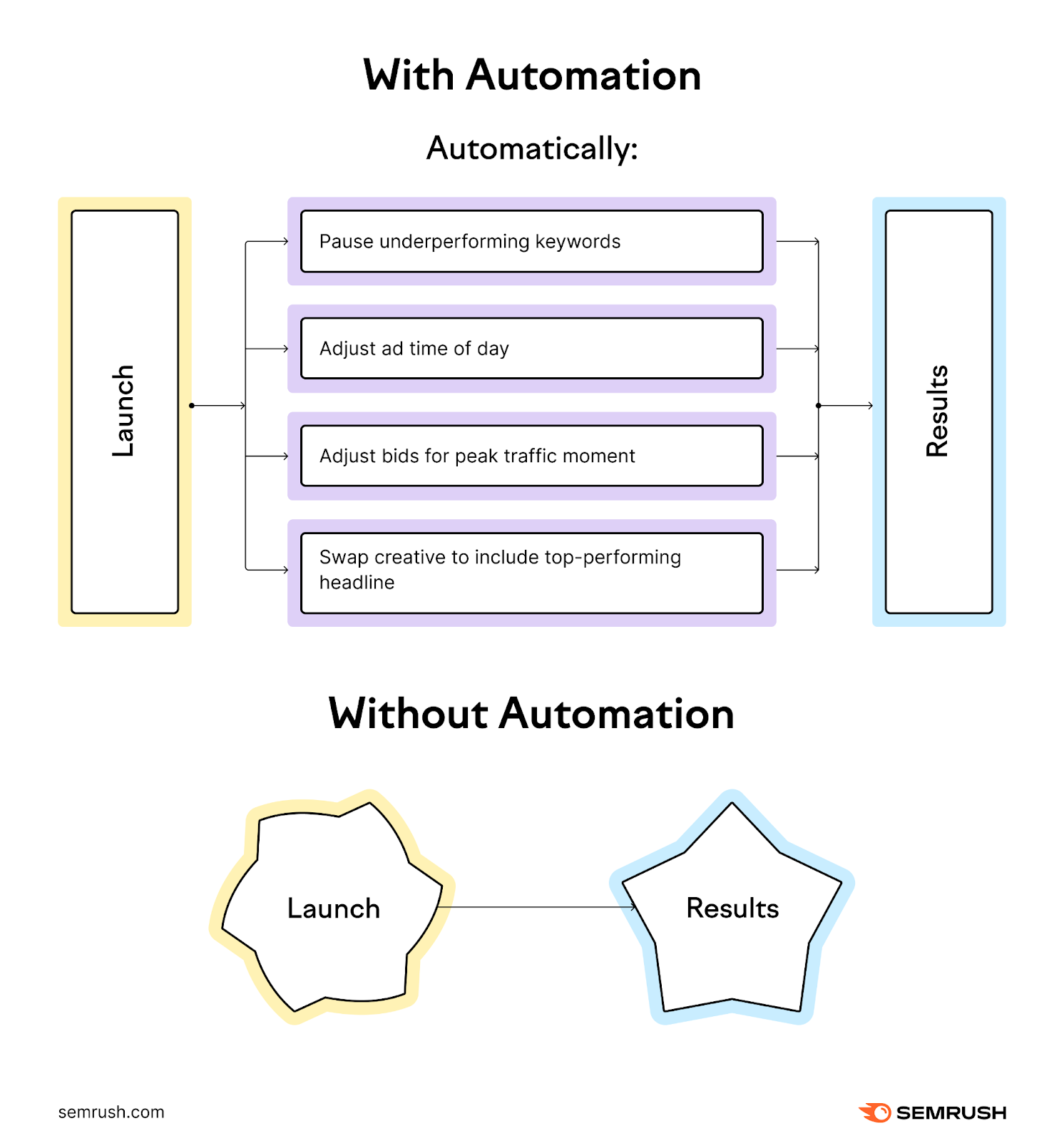
PPC automated bidding uses real-time data to adjust your bids automatically. If, for example, there’s a spike in searches for your product on weekends, the system can automatically increase your bid during that time.
This approach eliminates the need for you to monitor and adjust bids constantly.
With automated bidding, you can optimize your budget, reduce human error, and ensure your ads connect with the right audience when they’re most likely to engage.
How to Get Started with Automated Bidding
Here’s a breakdown of Google Ads’ popular automated bidding strategies:
- Maximize clicks: Sets your bid to maximize the number of clicks your ad gets while staying within your budget
- Enhanced cost per click (ECPC): Automatically adjusts your bids to get clicks that are more likely to convert
- Maximize conversions: Automatically adjusts bids to encourage as many people as possible to take your desired action
- Maximize conversion value: Uses automation to optimize your bids so they drive high-value conversions
- Target CPA: Controls total budget by letting you set how much you want to spend on each action
- Target return on ad spend (ROAS): Allows you to maximize outcomes by setting a specific goal for how much return you want to get on your ad spend
Which bidding strategy is right for you depends on your goals for that specific campaign.
For example, maximizing clicks might be best if you’re aiming to boost brand visibility. But choosing a target return on ad spend is more appropriate if you’re focused on getting a specific return for every dollar spent.
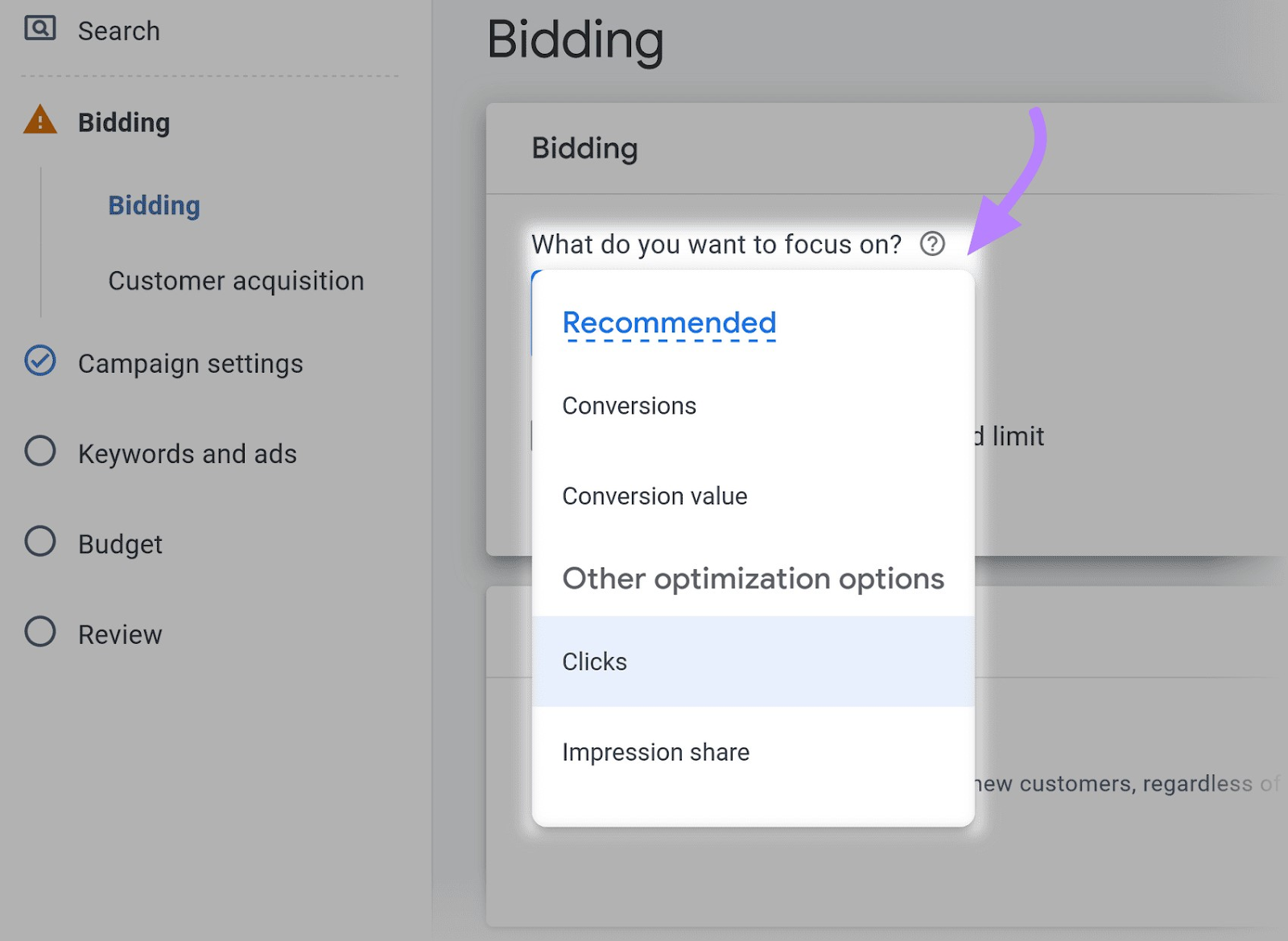
Once you’ve decided which bidding strategy you want to use, here’s how to implement it.
Log in to Google Ads.
Select “Campaigns” from the menu on the left.
Click on the name of the campaign you’d like to edit.
Then, in the “Bidding” menu, you’ll find the option to choose your automated bid strategy.
Creative Testing
Testing ad variations helps identify which combinations of headlines, descriptions, and/or images engage your target audience most effectively.
However, doing this manually can be tedious and the process is prone to errors.
Automating creative testing simplifies this by pinpointing the top performers based on real-time analysis of different ad combinations.
For instance, in search ads, if one headline and description combination consistently outperforms others during weekday afternoons, Google will prioritize showing that combination during those times.
This ensures consistent ad optimization. Saving you hours of manual work and increasing your campaign’s effectiveness—especially if you’re running multiple ads.
How to Get Started with Automating Ad Creative Testing
You need to have multiple variations of your ad creative. Upload them on the ad platform.
Go to Google Ads and create a new search ad campaign. You will find the option to input multiple versions of headlines and descriptions.
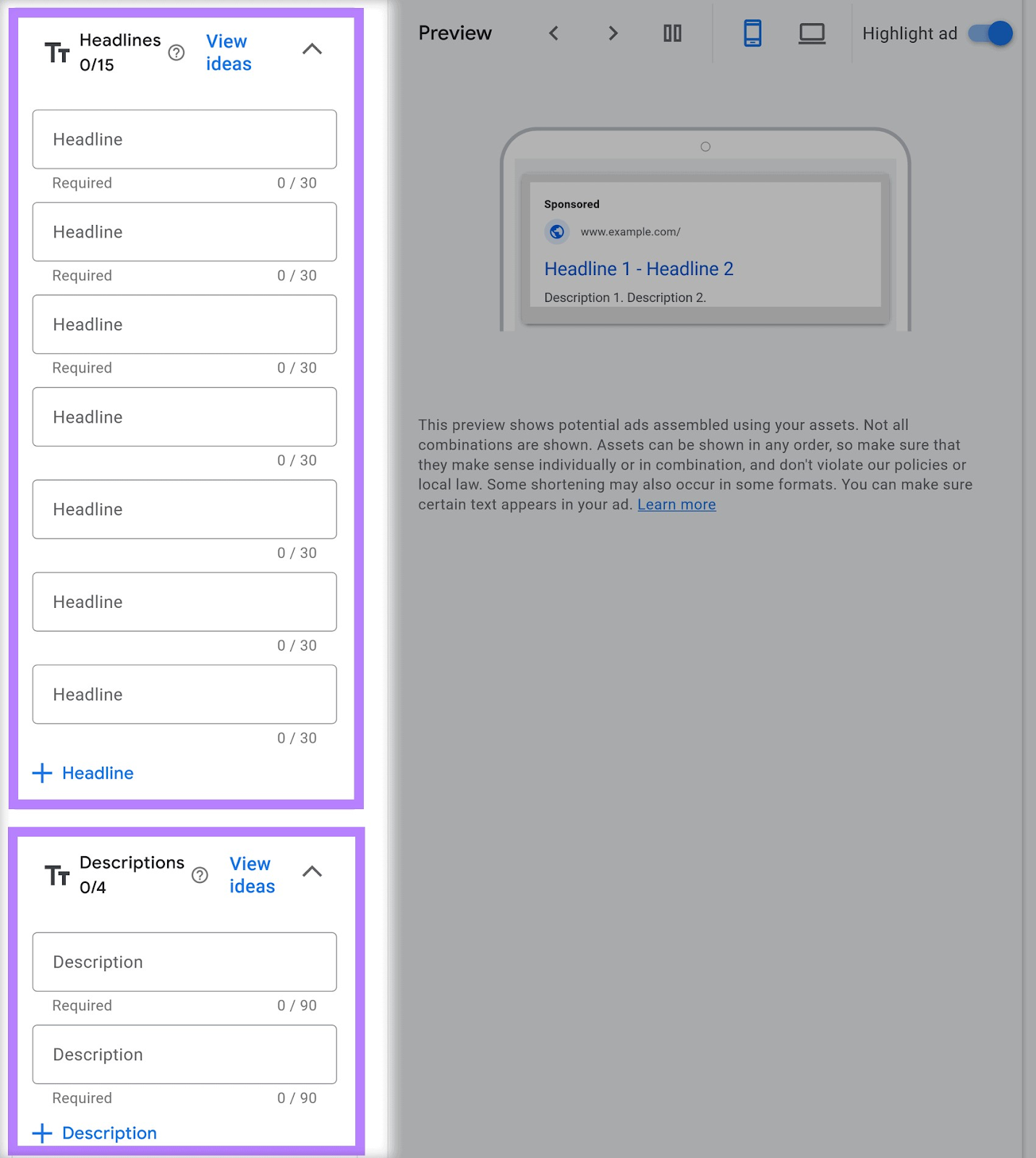
This feature enables the ad platform to test different combinations automatically and show the one most likely to be effective for your target audience.
Once your campaign is live, the platform will continuously monitor performance. And automatically adjust which creative elements are shown based on real-time data.
Campaign Management
Campaign management involves planning, executing, and monitoring your PPC campaigns. It’s where you select keywords, set bids, choose creatives, and track performance.
Automated PPC management tools make managing your PPC campaigns more efficient.
It allows you to automatically monitor campaign performance in real time and make adjustments based on predefined criteria.
For instance, you can set a rule that if a campaign’s click-through rate drops below a certain threshold, it will automatically pause. And if a campaign is performing well, automation can increase your bid to capitalize on its success.
How to Get Started with Automated Campaign Management
Start by reviewing what part of campaign management you want to automate. Look for areas that require frequent adjustments.
Next, go to Google Ads and head over to the “Tools” tab.
Click “Bulk actions” and choose “Rules” from the drop-down menu.
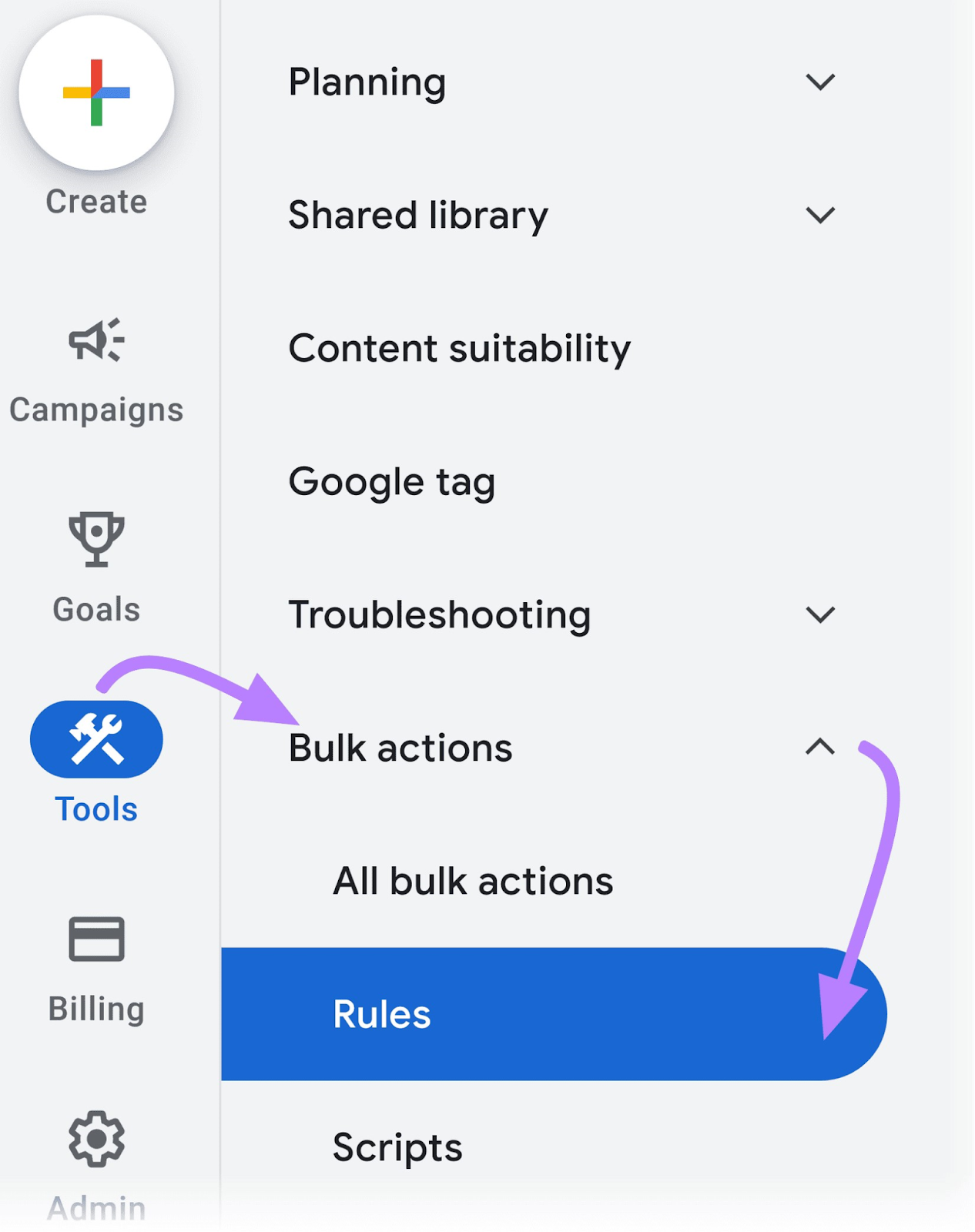
Now create your automated rules. You will find numerous ways to automate your campaign in the menu.
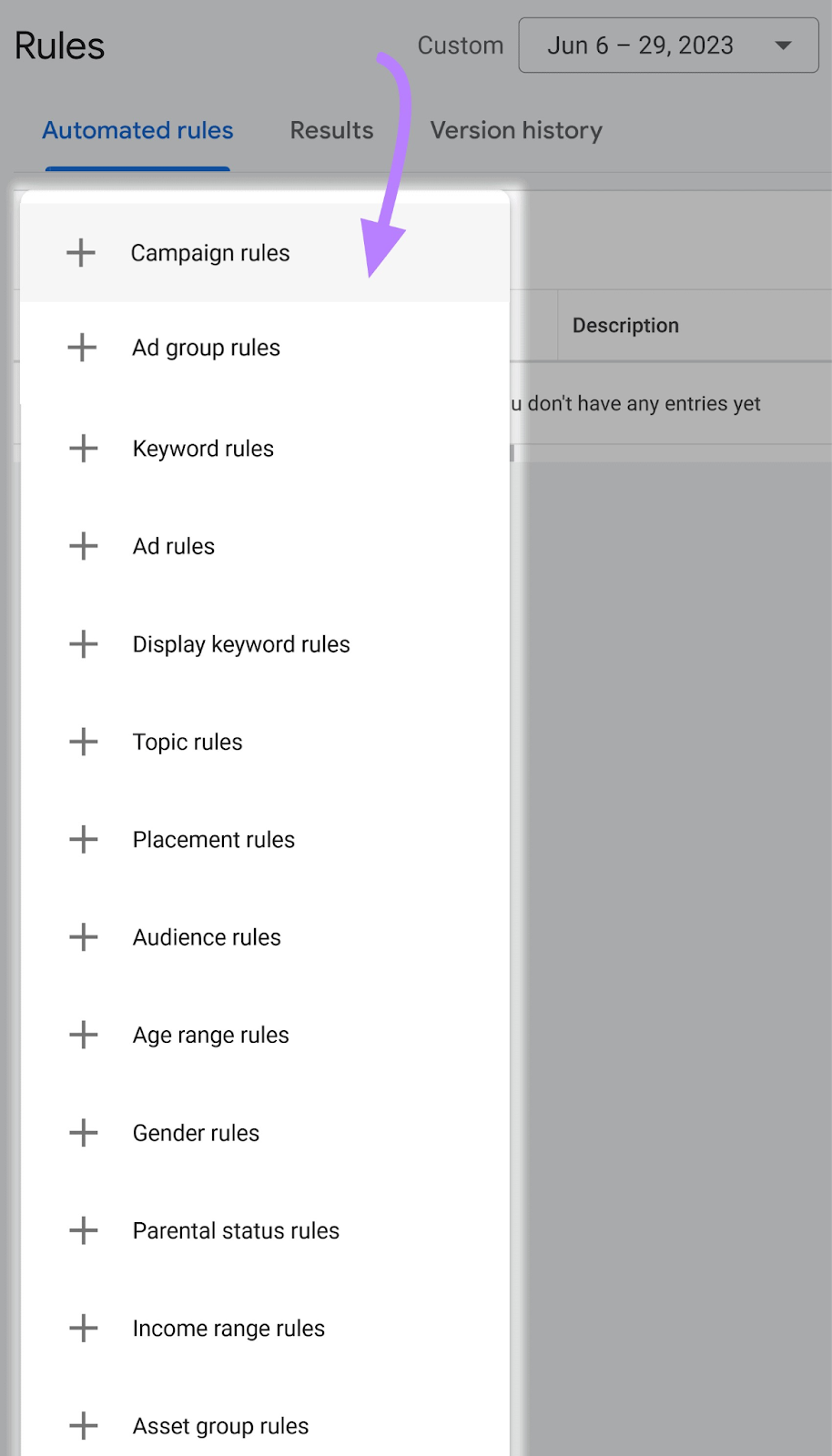
Let’s say you typically make more sales on the weekends. So you want to automate PPC budgeting to increase your campaign budget on Friday, Saturday, and Sunday to reach more people.
Here, you need to create two rules:
- One will help increase your budget on Friday
- Another one will bring your budget down to the original sum on Monday
Click “Campaign rules” and configure your automation rules.
Under “Action,” choose “Change budgets” and set your increased budget for the weekend.
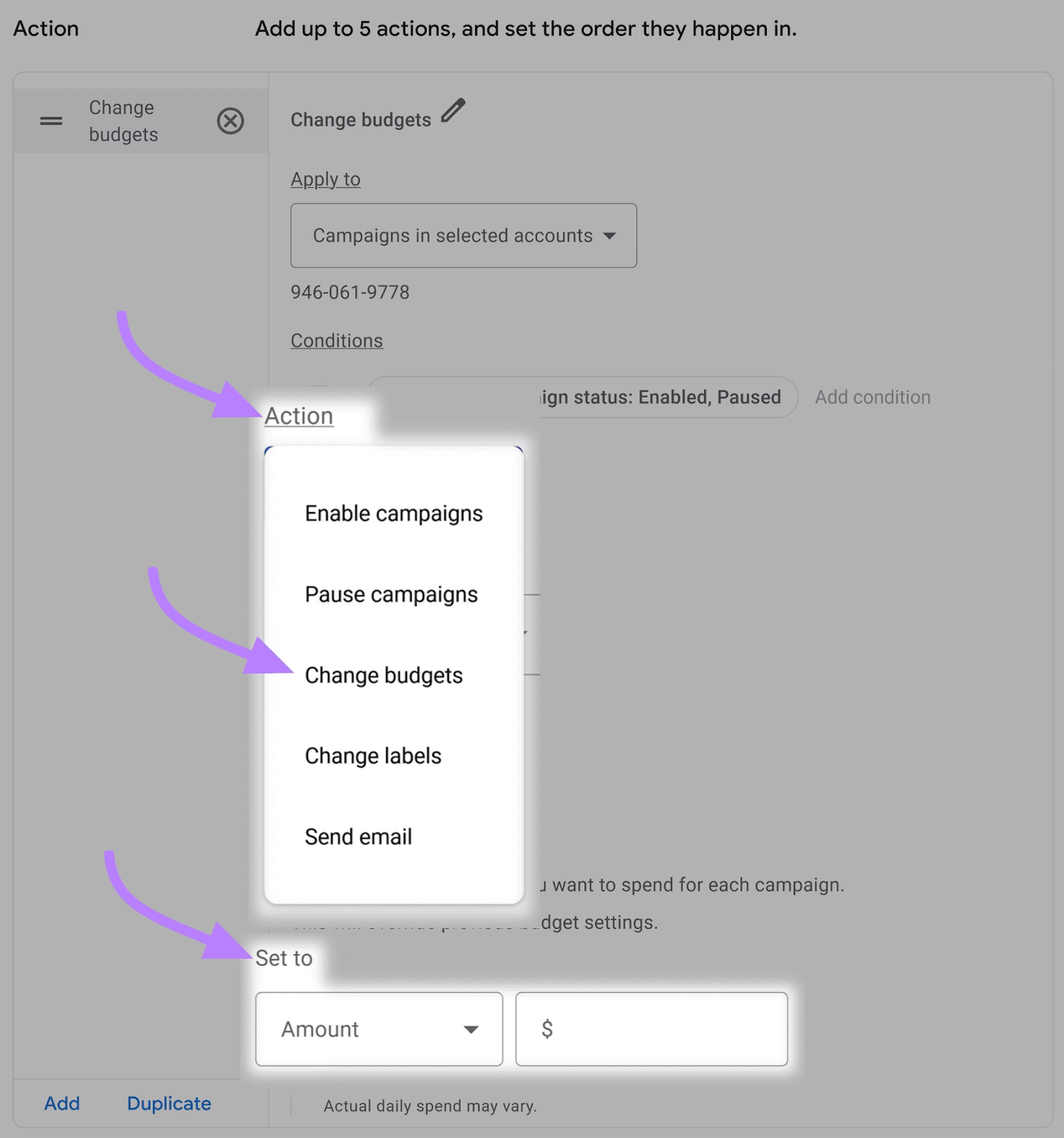
In the frequency, select “Weekly” > “Friday.” And choose the time “12:00 AM - 1:00 AM.”

Save the rule. This will increase your budget every Friday.
Follow the same steps to set your second rule, which will bring your budget back to normal every Monday.
Once set, your ad budget will automatically increase and decrease on the selected days.
Similarly, you can create other automated rules based on your needs. From scheduling higher bids during specific hours of the day to pausing ads based on specific metrics.
Audience Targeting
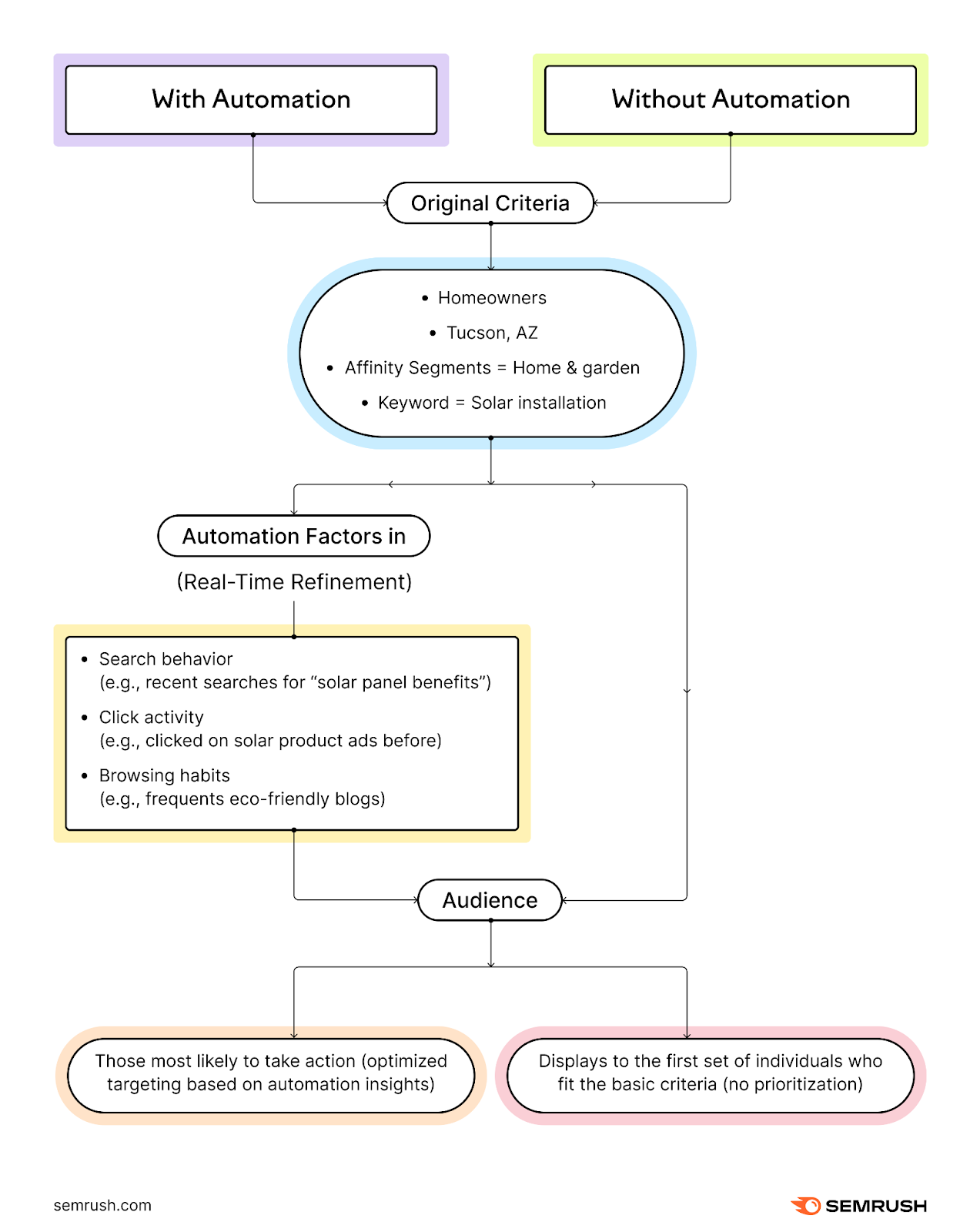
Automated audience targeting leverages machine learning to dynamically adjust the audience segments your ads are targeting.
This ensures your ads are displayed to the individuals most likely to engage with them.
For example:
If the data shows that a younger demographic is interacting more with your ads, the system can reallocate more of your budget to target that specific age group.
By automating the audience-targeting process, you’re not just setting and forgetting; you’re continually optimizing, which leads to better ROI.
How to Get Started with Automated Audience Targeting
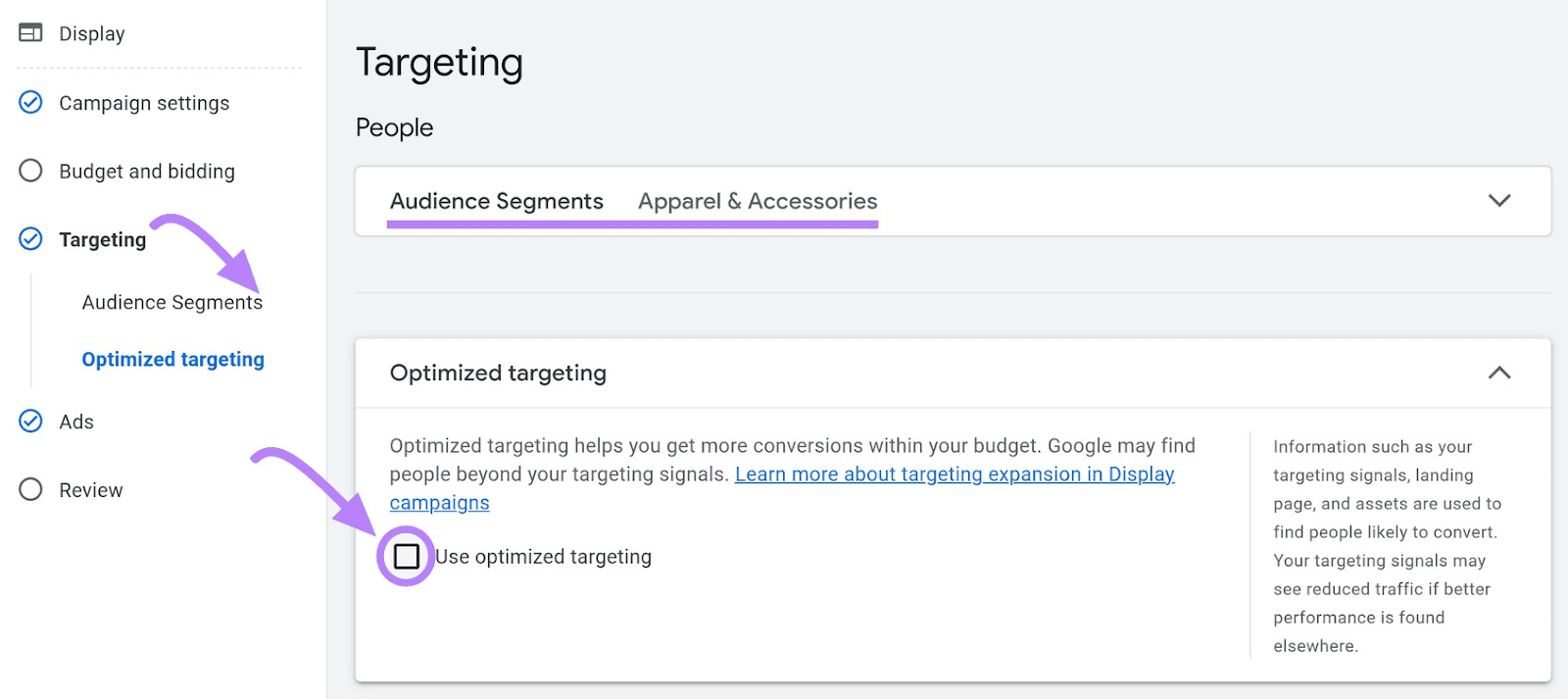
You can automate your PPC display ads using the Optimized targeting feature in Google Ads.
It uses real-time conversion data (users who have converted) to create similar profiles of other users. It then improves your campaign’s performance by displaying ads to audiences that match that profile.
Optimized targeting can help you reach audience segments more likely to convert.
It is turned on by default for all campaigns. You can turn it off in ad group settings, under “Targeting” > “Audience segments.”
Reporting
Automated reporting streamlines the collection and presentation data from your PPC campaigns.
Reports are generated at regular intervals, saving you time by removing the need for manual report creation.
Automation also eliminates human errors during manual data collection and interpretation.
For example, if you want to track the performance of a particular campaign every Monday morning, automated reporting can have that data ready for you right at the start of the week.
With PPC report automation, you get accurate, timely insights without the manual hassle. This lets you make informed decisions quickly and keeps your campaigns effective.
How to Get Started with Automated Reporting
You can automate your reporting process using Google Ad Manager’s scheduling feature.
This feature allows you to set up reports to be generated at specified intervals, ensuring you receive timely insights tailored to your needs.
Go to your Google Ad Manager account and click “Reports” from the top navigation.
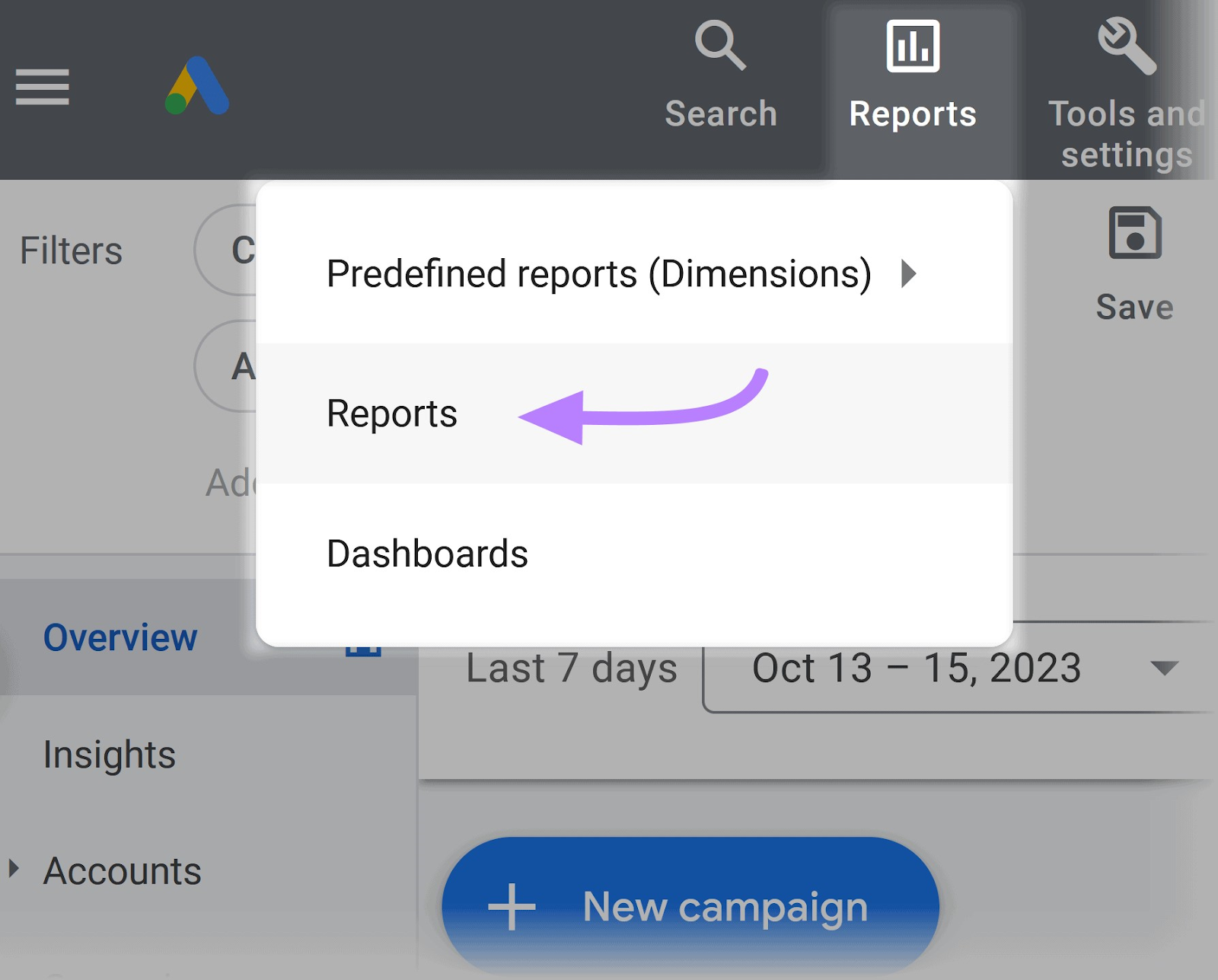
Create a new report or edit an existing one. Navigate to the “Editors and scheduling” section and schedule your report.
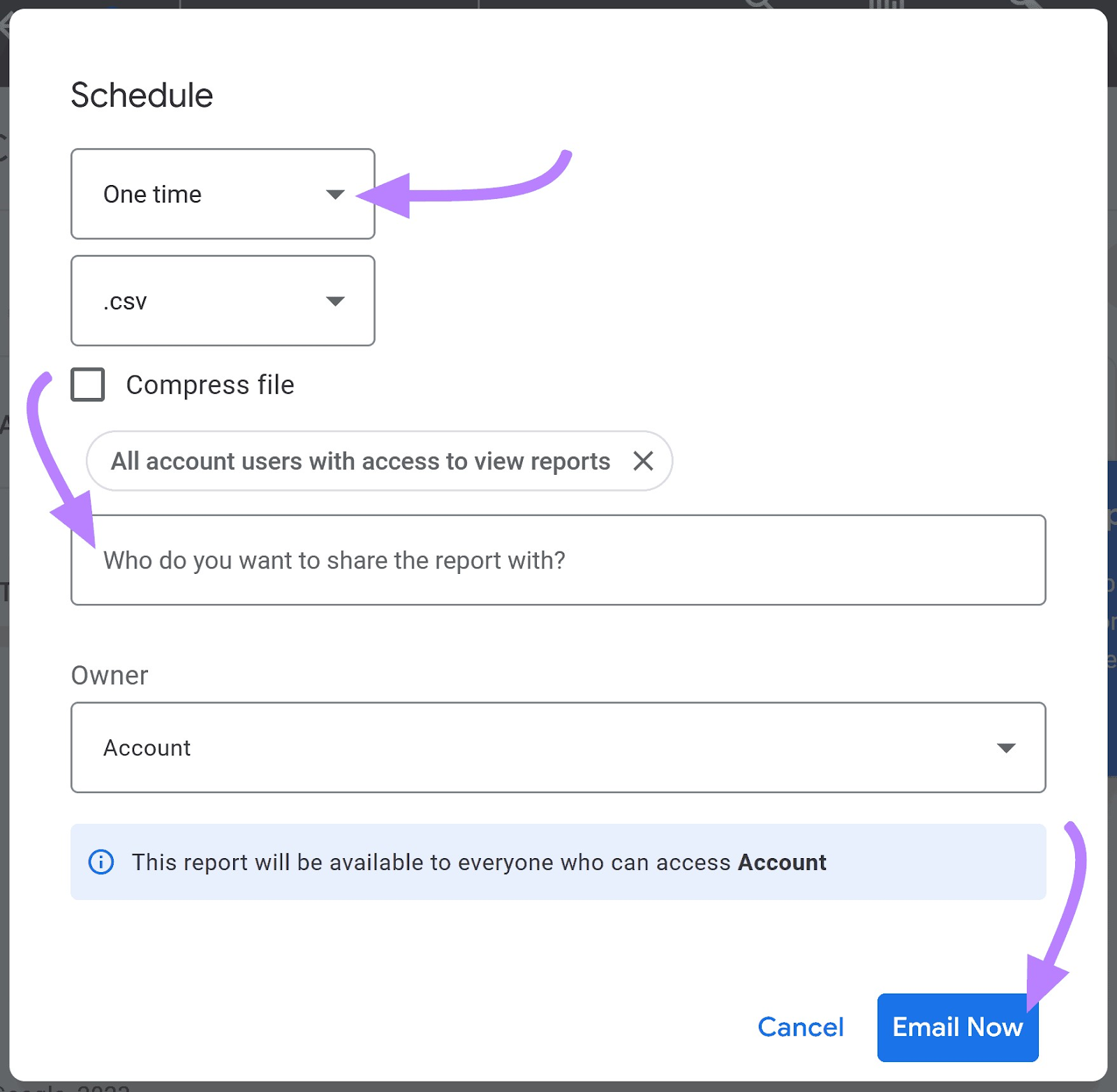
You can choose the frequency and date range of the scheduled report—when and how often you want the report emailed.
You can also share the reports with your team members and external stakeholders.
3 Other Types of PPC Automation Tools
Beyond the built-in automation features provided by Google Ads, you can use three other types of PPC automation tools based on your use case.
Let’s take a look at each type.
1. Scripts
Scripts are custom code snippets (usually written in JavaScript) that you can add to your ad platform in order to automate more complex tasks.
This option requires a certain level of coding skill and a deep understanding of the ad platform’s functionalities.
Google Ads offer a library of pre-made scripts. For example, it has a source code to bid based on current weather.
There are a number of pre-made scripts available online. Usually for free.
You can even experiment with writing your own using tools like ChatGPT.
2. Third-Party Tools
Third-party tools (which we’ll cover more in the next section) include PPC automation software solutions developed by companies other than the ad platforms themselves. You can typically subscribe to them with monthly recurring charges.
These tools offer advanced automation features, ranging from budget distribution to reporting.
They’re designed for those who need more sophistication than built-in features and scripts can offer. They are often used to manage campaigns across multiple ad platforms.
3. Custom Builds
Custom builds are PPC automation software programs tailor-made by developers.
This approach is most suitable for large companies with unique PPC needs that can’t be met by existing tools.
It requires significant development expertise and resources but offers the most customization.
5 Third-Party PPC Automation Tools to Try
Let’s take a look at some of the best PPC automation software tools from third-parties:
1. Position Tracking
Position Tracking helps you monitor search ad positions on Google. To ensure you’re always in the loop on how your ads are performing.
Open the tool, enter your domain, and click “Set up tracking.”
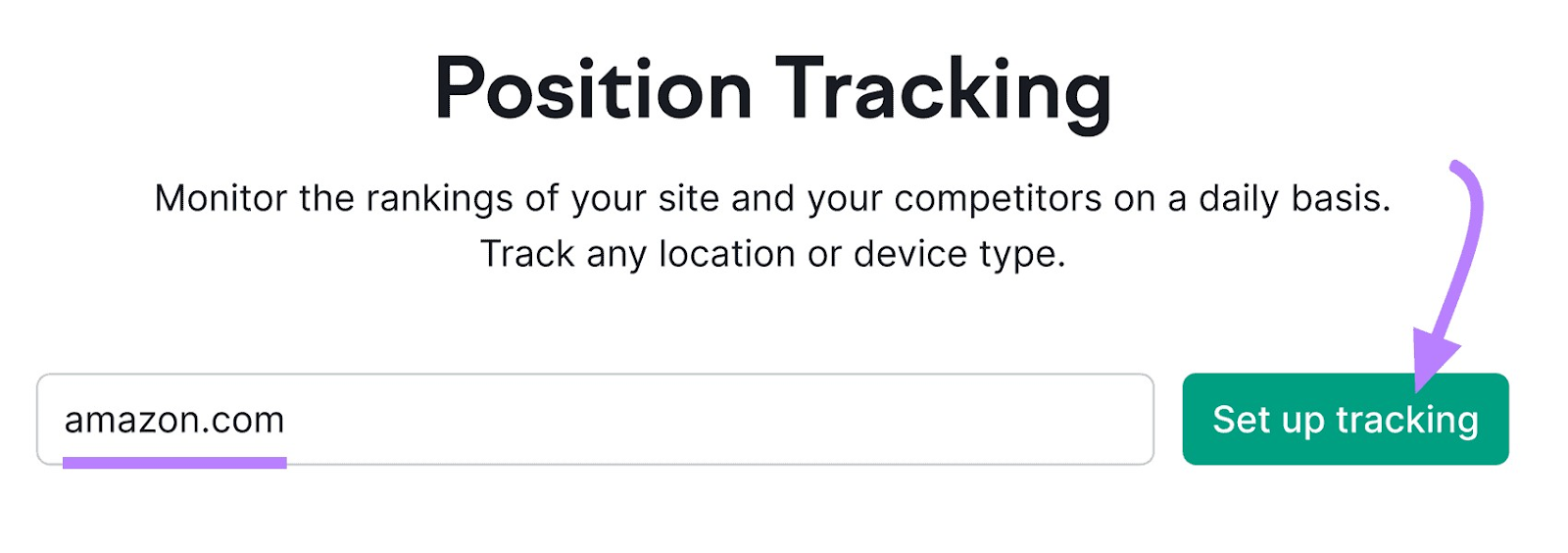
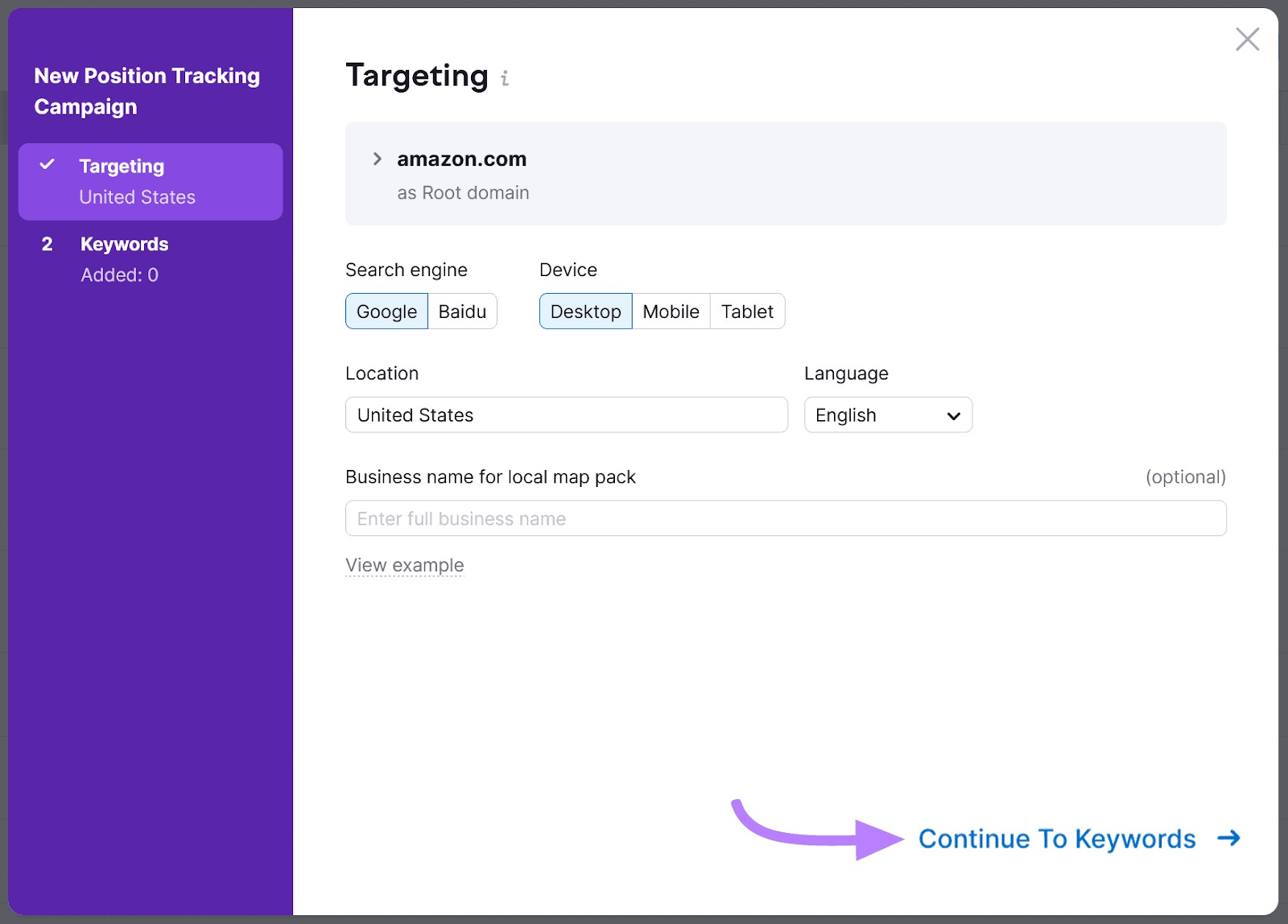
Follow the targeting steps. Then, click “Continue To Keywords.”
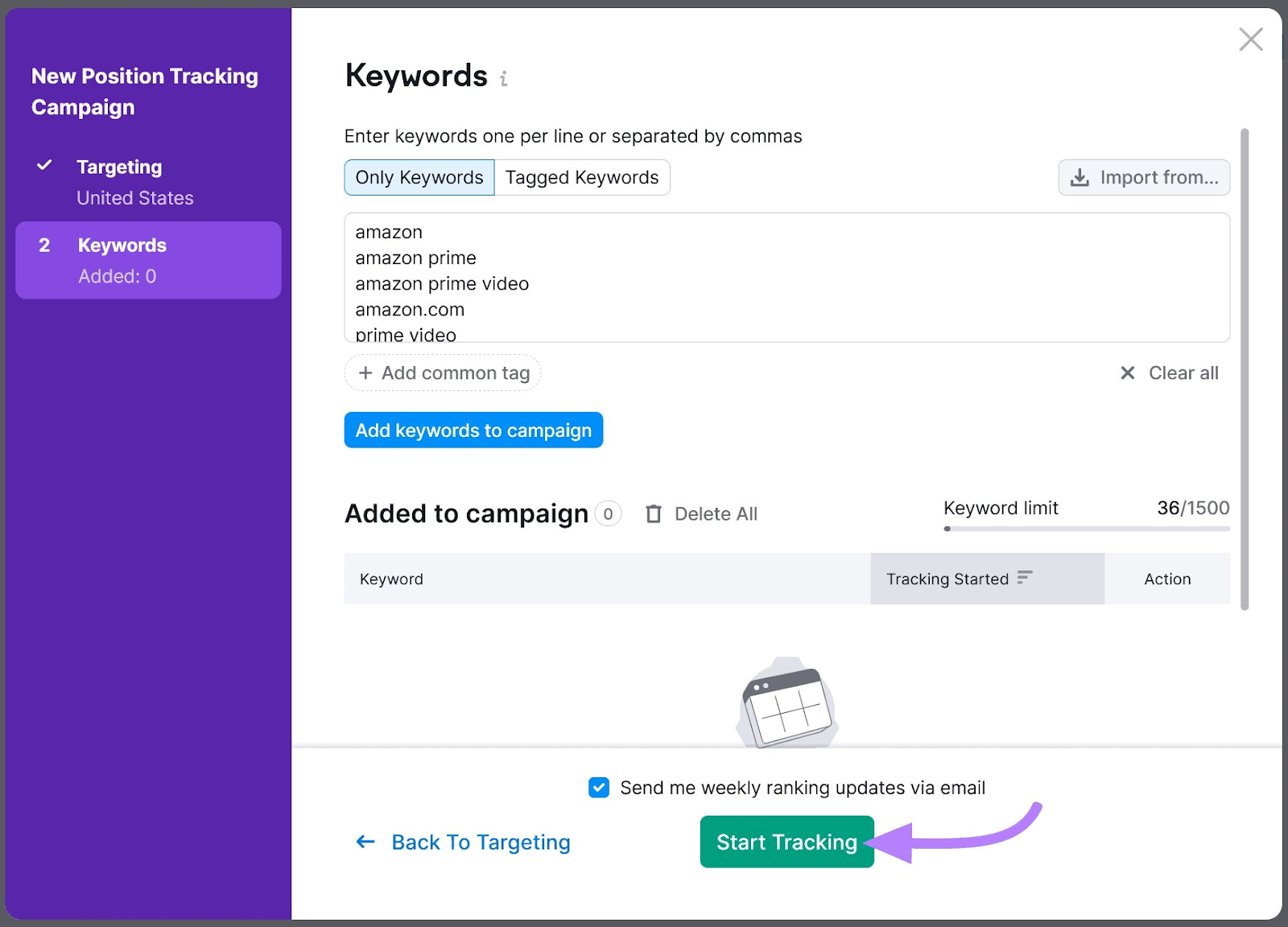
Add the keywords you want to track (the ones you’re bidding on). Then, click the “Start Tracking” button.
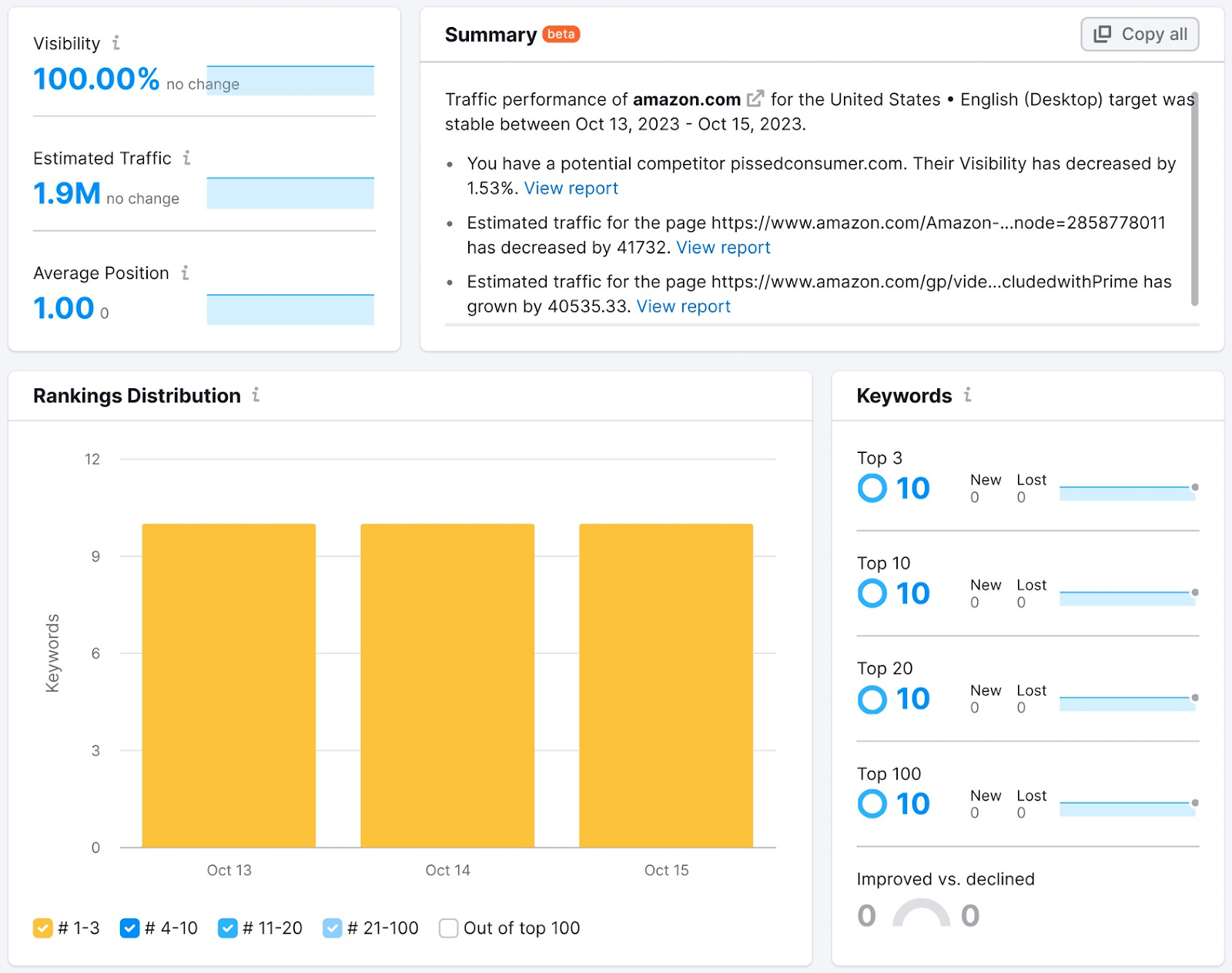
Once the tool is ready, you’ll see the main dashboard.
Click the settings icon in the top-right corner and select “Google Ads” under “Type.”
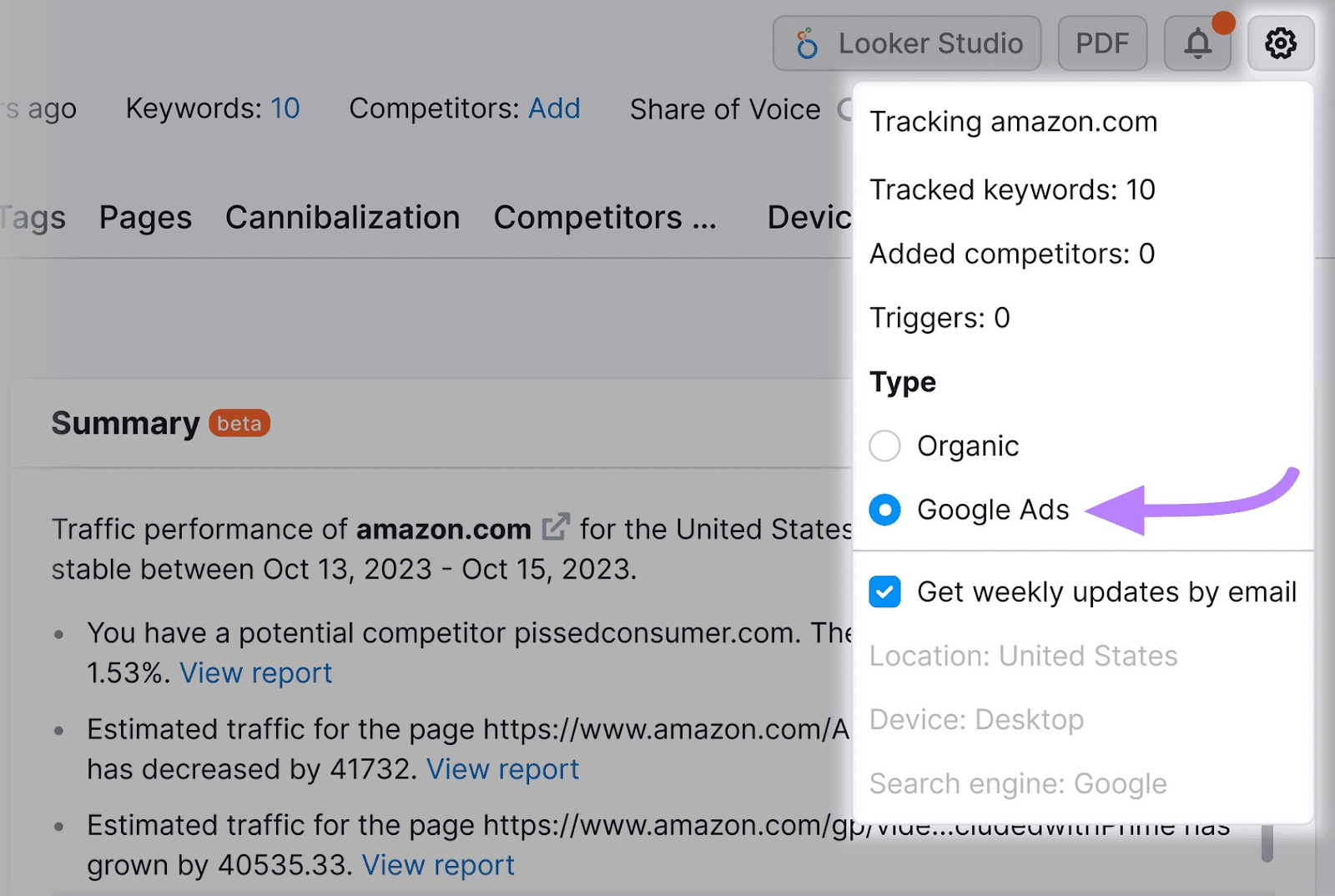
You’ll now see data related to the keywords you’re bidding on in your campaigns.
Navigate to the “Overview” tab. Scroll down to the “Rankings Overview” section. And click the “Positions” button to see which keywords your ads are ranking for and their ranking position.
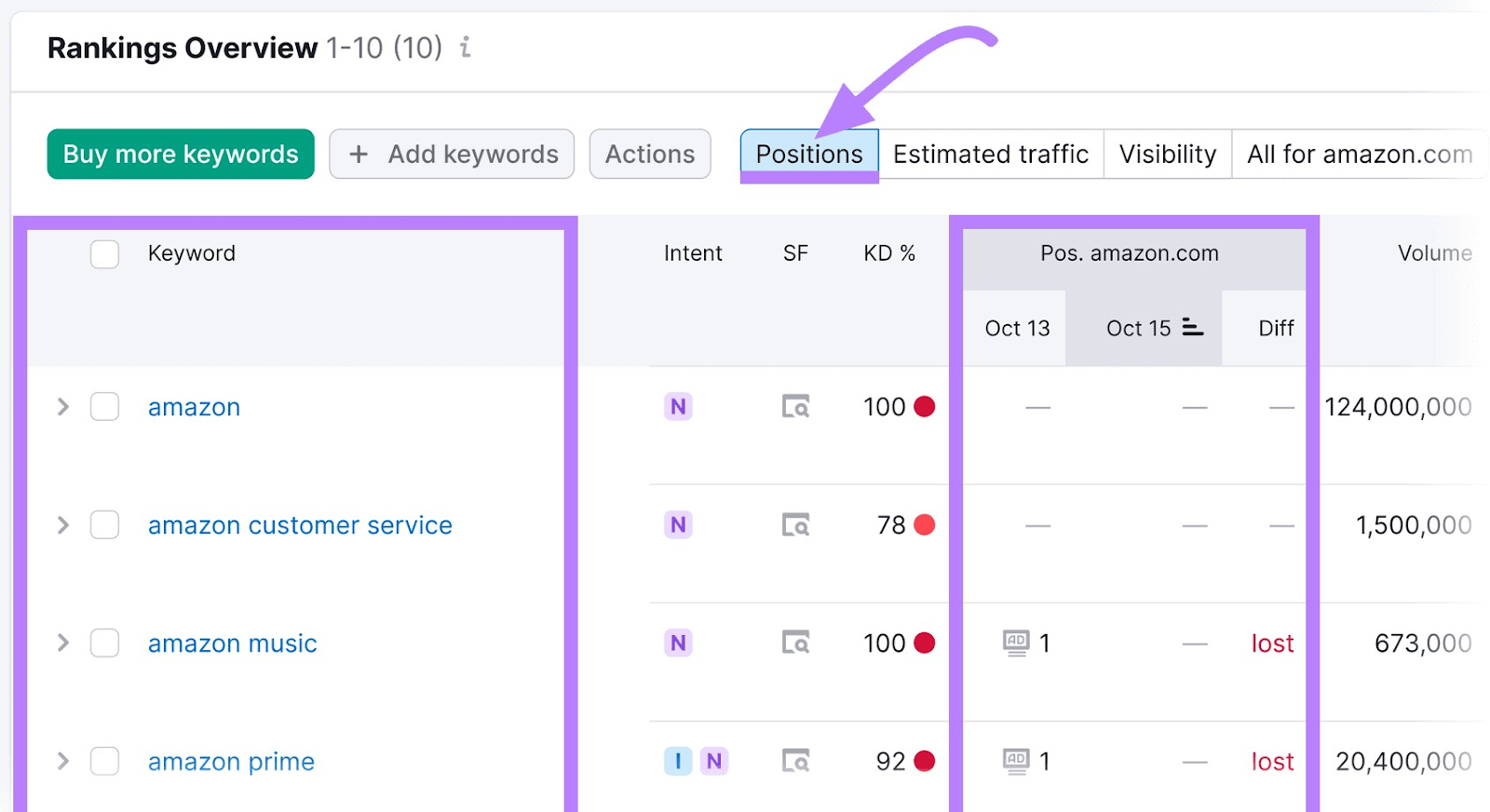
You can also set up custom alerts that notify you of significant changes.
To set up your alerts, click the settings icon in the upper-right corner of the page. Then select “Triggers.”
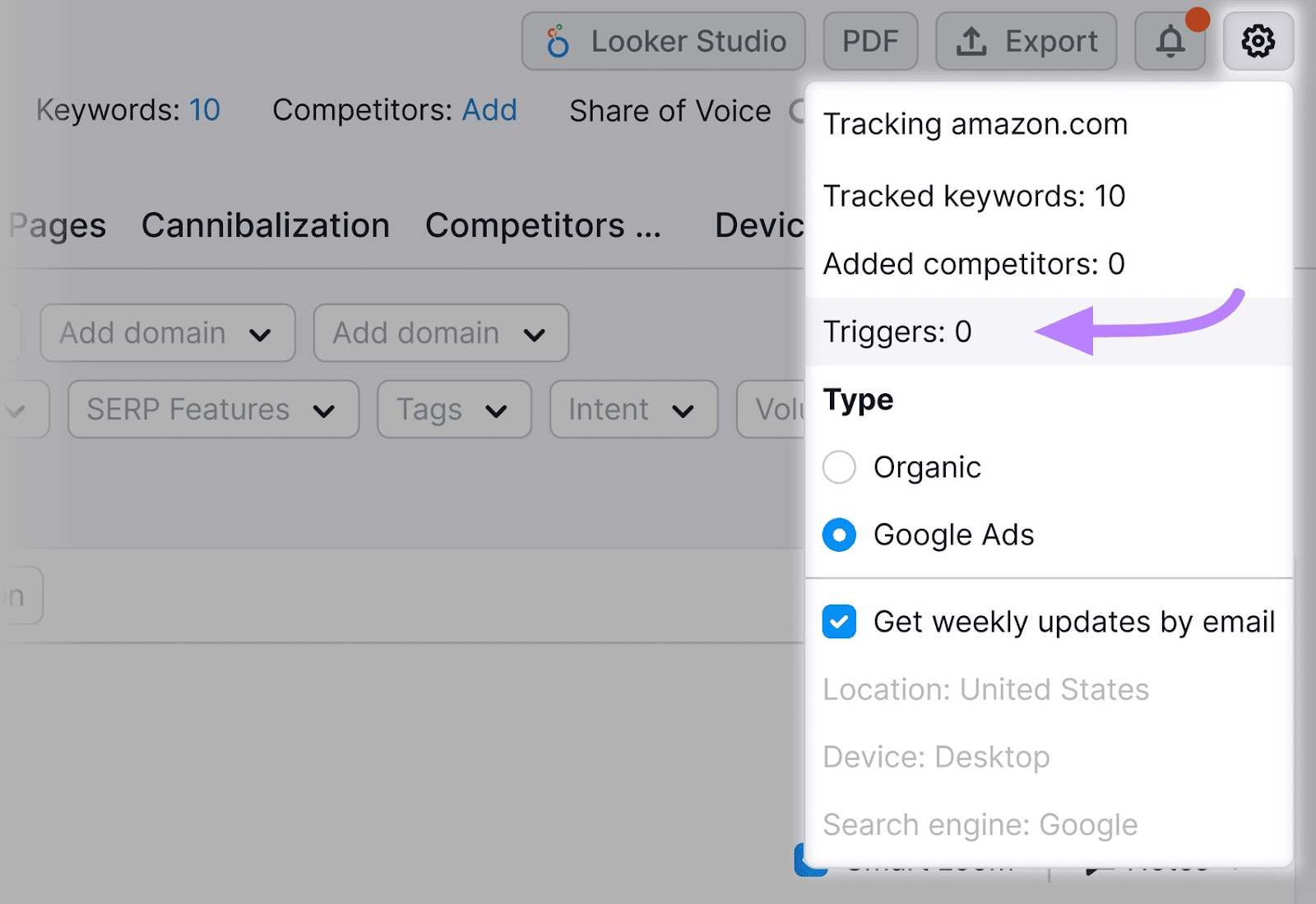
Then click the “Add new trigger” button.
Use the drop-down menu to select the desired trigger event you’d like to set up. Then click “Add.”
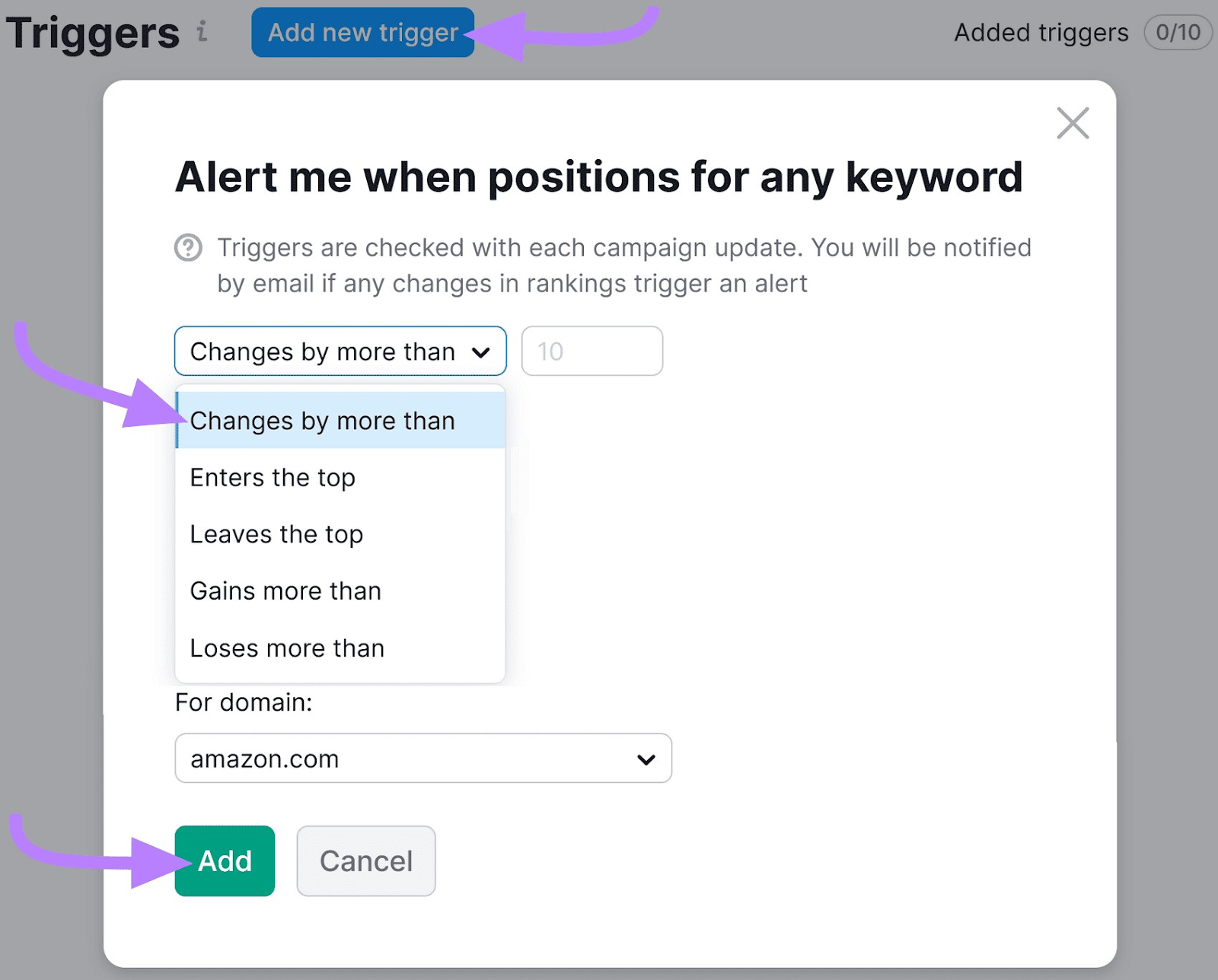
You’ll now get an email anytime a ranking change triggers a saved event.
Position Tracking has other features and capabilities too, like advanced filters and custom notes. It can also be used to track your competitors’ ad positions.
Pricing: You can sign up for a free account to get limited access to Position Tracking and other Semrush tools. Paid plans start at $129.95 per month. Check out our full pricing details.
2. AdEspresso
AdEspresso makes it easier to set up multiple ad variations for A/B testing on platforms like Facebook, Instagram, and Google Ads. To determine which ads and target audiences work best for you.
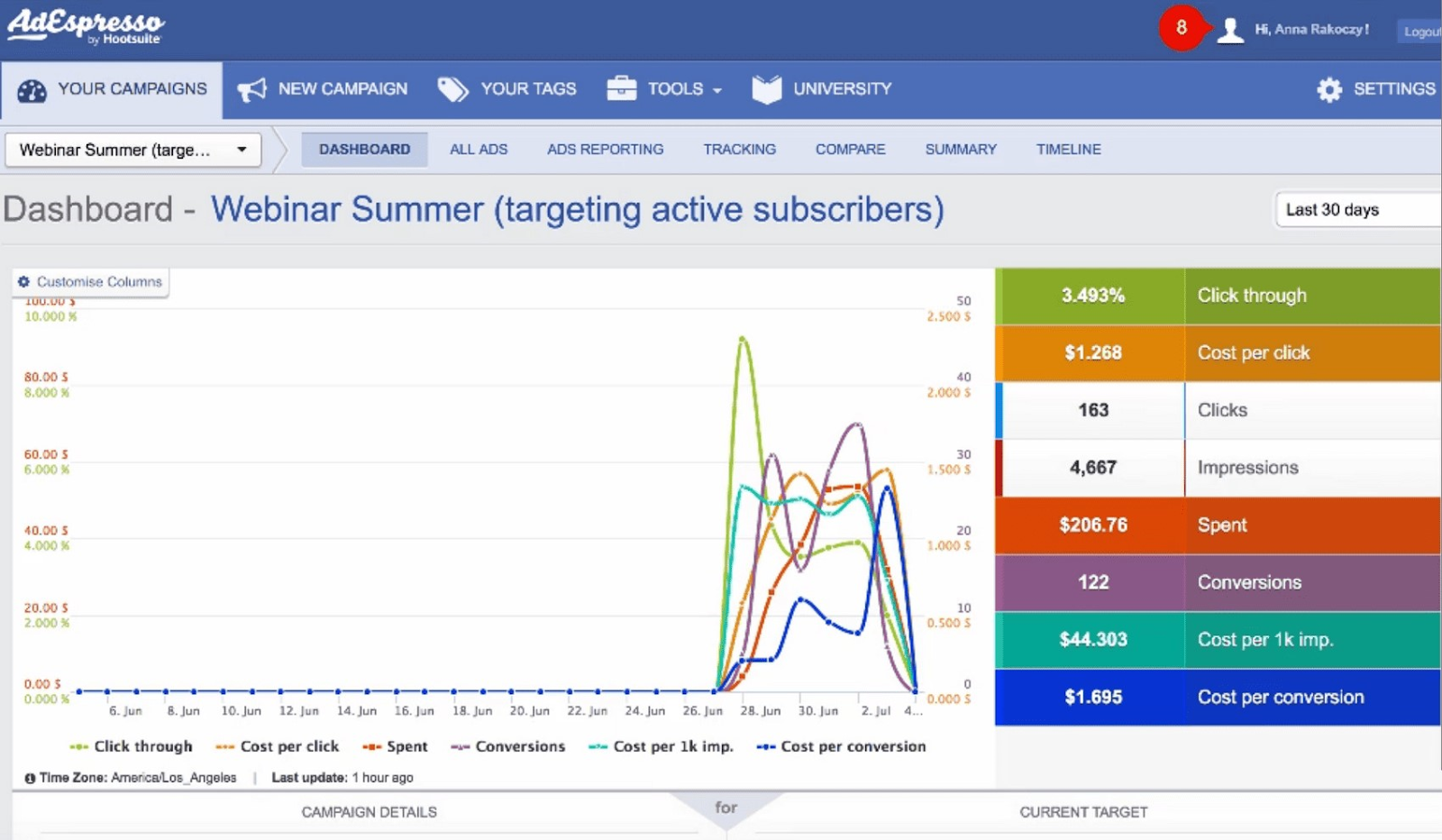
Image Source: AdEspresso
AdEspresso can automate various aspects of your ad campaigns. Like testing ad copy, scheduling, and more.
AdEspresso can automatically stop ads that aren’t performing well. And reallocate your budget to better-performing ads.
It also provides easy-to-understand analytics dashboards. And custom reports with metrics that you want to track.
Pricing: Plans start at $49 per month. And there’s a free 14-day trial.
3. Swydo
Swydo is an example of automated PPC reporting software. It integrates with over 30 marketing platforms, including Google Ads and Facebook Ads—consolidating all your campaign data centrally.
The tool streamlines your reporting by allowing you to schedule reports to be delivered weekly or monthly. Or even generate on-demand reports when needed.
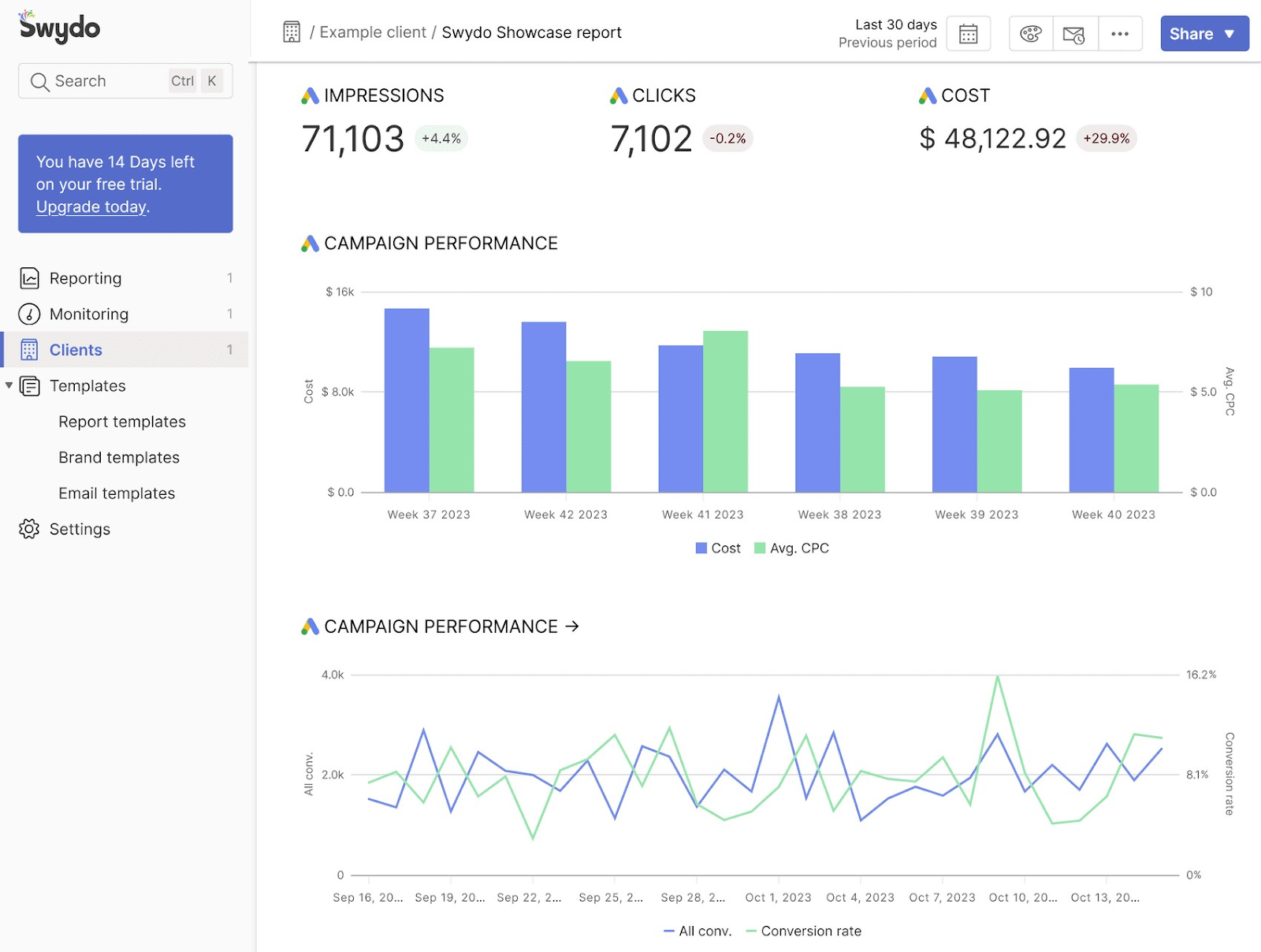
Swydo automates data collection and presentation, so you don’t have to pull numbers from different platforms manually.
It offers white-labeling options, which let you customize reports to align with your brand’s look and feel. Or to ensure they’re aligned with your client’s branding and specific needs.
Pricing: Plans start at $49 per month. And there’s a 14-day free trial.
4. Adzooma
Adzooma helps you automate PPC ad campaigns across Google, Facebook, and Microsoft.
You can set rules to pause underperforming keywords, adjust bids based on performance, and manage your budgets based on your goals.
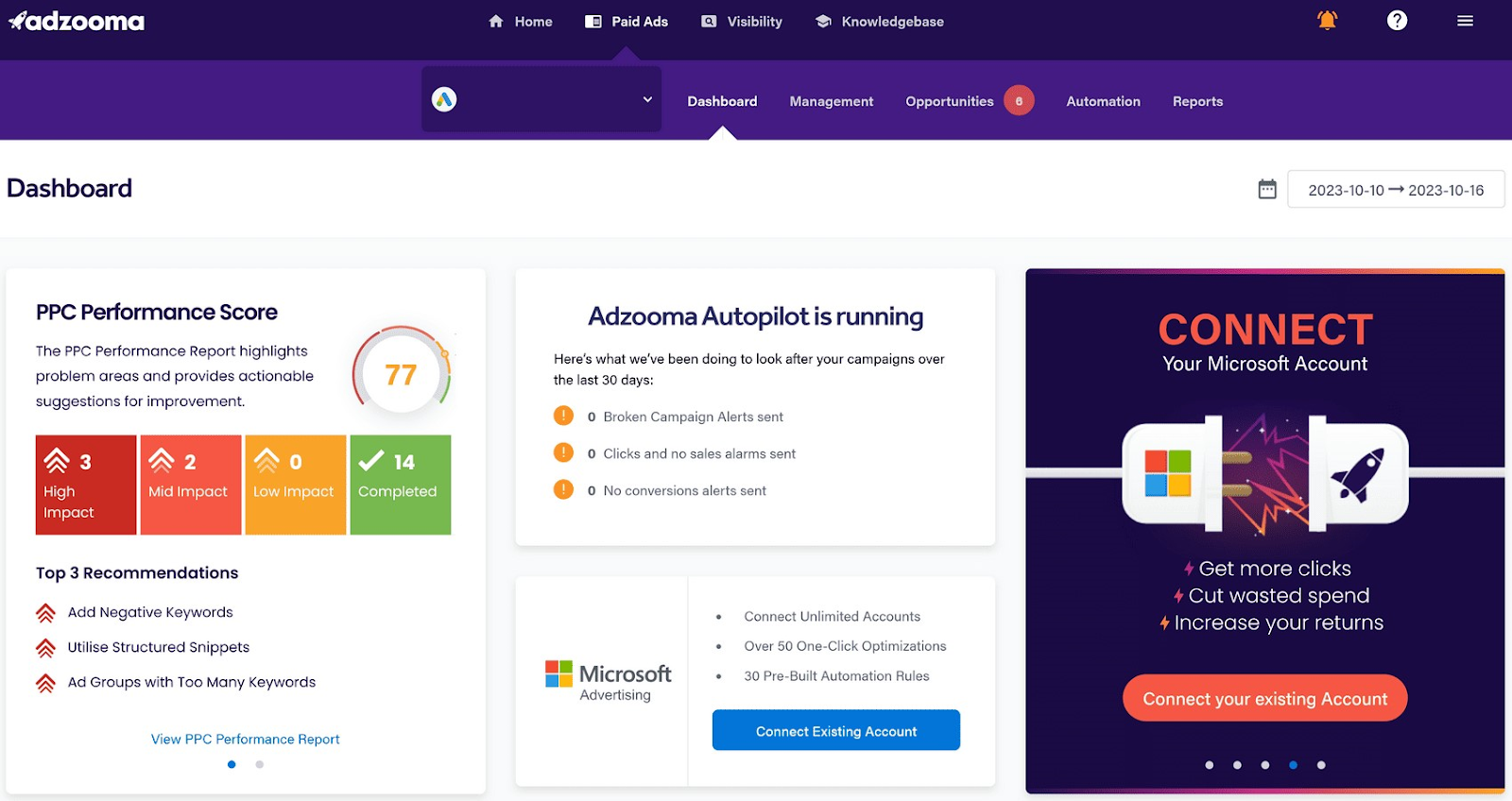
The tool uses machine learning to analyze your data for insights. To help you tweak your campaigns for better results.
Adzooma also offers alerts that notify you of key events. Like reaching a budget or pausing a keyword. So you’re always on top of your campaigns.
Pricing: This is a freemium tool. Paid plans start at $99 per month.
5. Adalysis
Adalysis is a PPC management software tool for Google and Microsoft Ads that offers a range of automation capabilities.
Its budget automation feature provides insights into your spending. And helps you choose the best budget allocation model for your campaigns.
The tool also sends real-time alerts based on your budget targets and changes.
Adalysis offers a suite of ad creation tools that allow you to create hundreds of campaigns in seconds.
You can use Adalysis to automate parts of your campaign reporting, A/B testing, auditing, monitoring, and optimization.
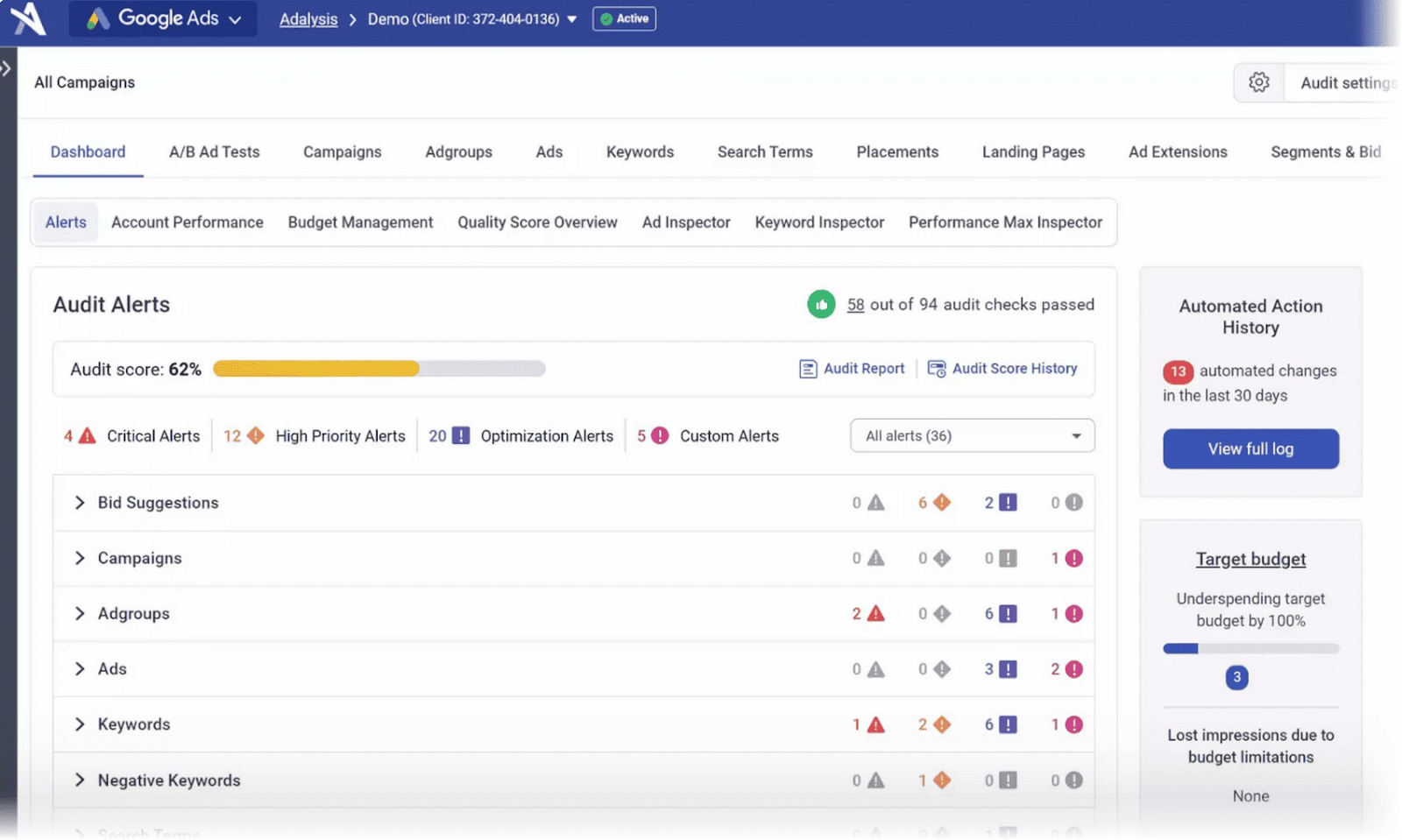
Image Source: Adalysis
Pricing: Plan prices vary according to your spend level and start at $99 per month. There’s a free 14-day trial.
Get Ready to Launch an Automated PPC Campaign
PPC automation can save you a lot of time. And potentially improve your returns.
But even before you automate your ad campaigns, you need to build a robust ad strategy. And this starts with a competitive analysis.
You can use Advertising Research for this.
Open the tool, enter the competitor domain you want to research, and click “Search.”

In the “Positions” tab (default), click “Keywords” in the “Paid Search Trends” widget.
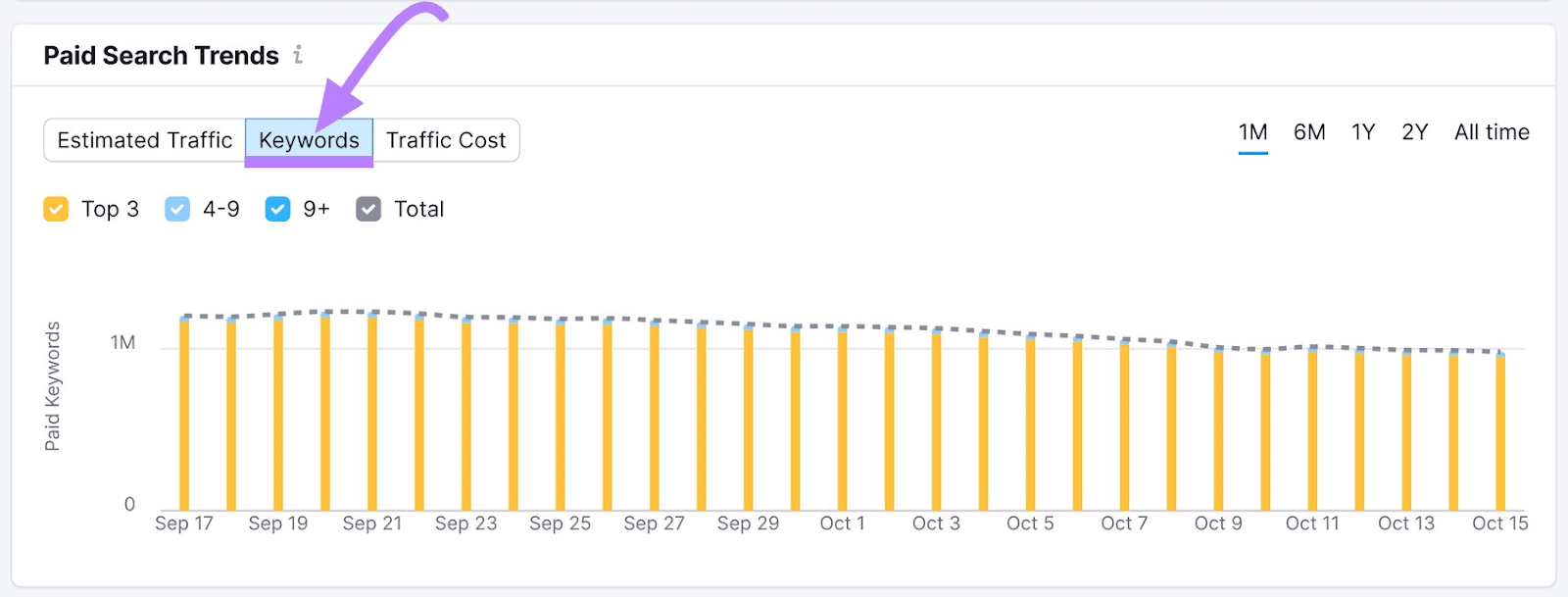
This will show you the total number of paid keywords their ads appear for.
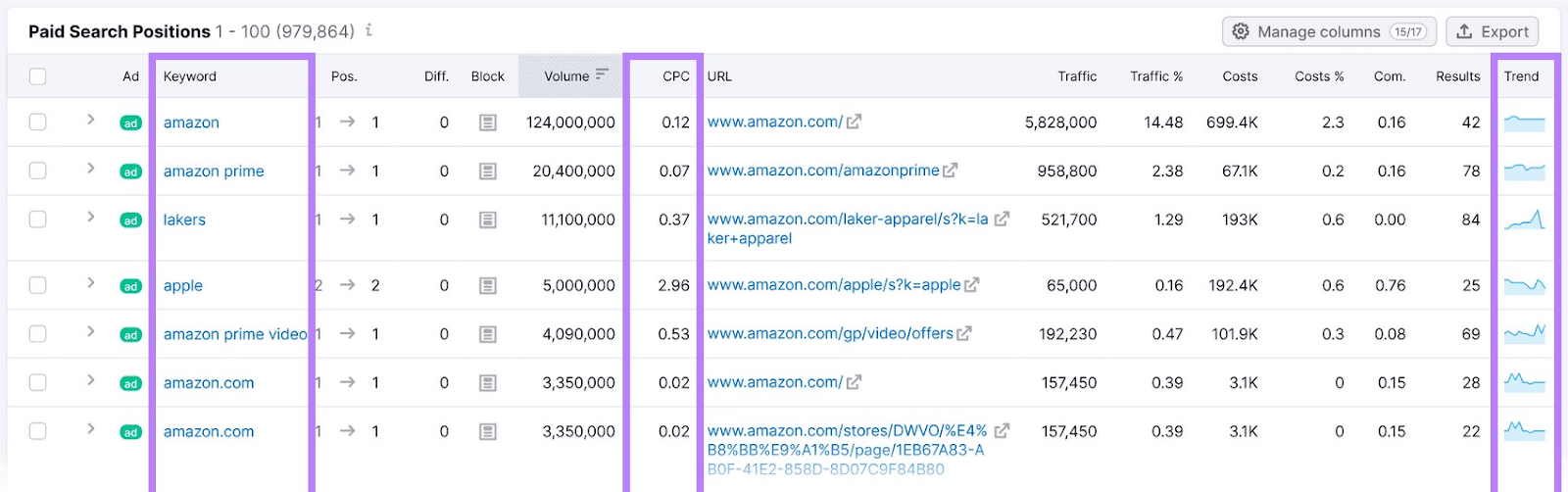
Scroll down to find the exact list of keywords. Along with other data points like cost per click and search interest trend.
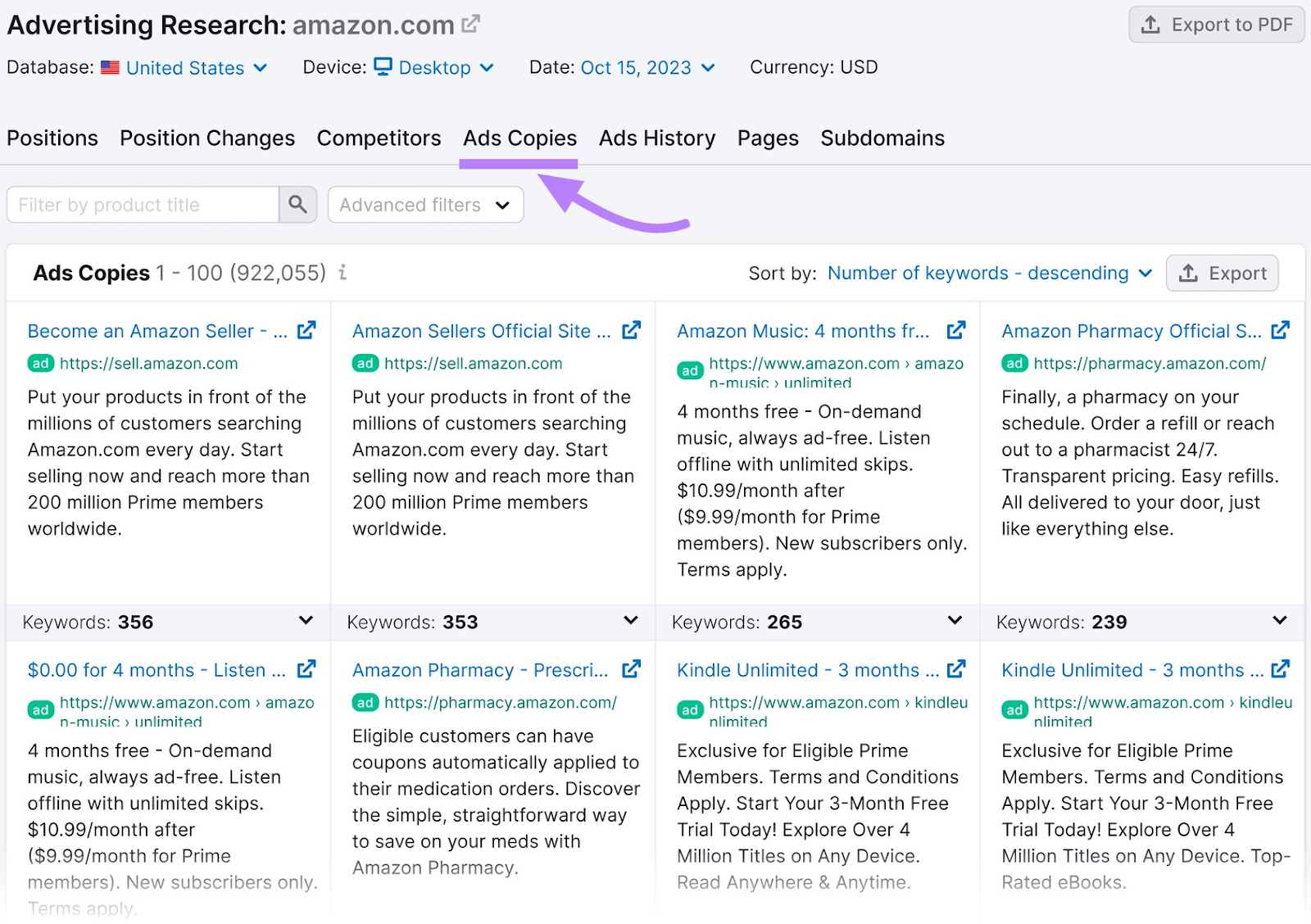
Next, click the “Ads Copies” tab to see your competitor’s actual ad copy and the corresponding keywords.
You can try Advertising Research for free. Sign up today.
